Axioma da escolla

(S_i) é unha familia de conxuntos indexada sobre os números reais ℝ, é dicir, hai un conxunto S_i para cada número real i, como se mostra cunha pequena mostra. Cada conxunto contén algún elemento, posiblemente un número infinito. O axioma da escolla permítenos seleccionar un único elemento de cada conxunto, formando unha familia de elementos (x_i) tamén indexados segundo os números reais, con x_i tomados a partir de S_i. En xeral as coleccións poden indexarse segundo calquera conxunto I, non só ℝ.

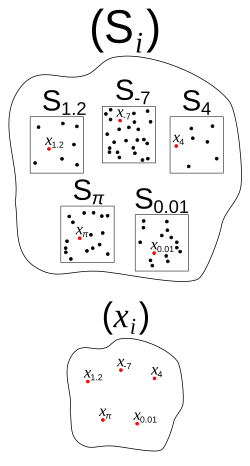
En teoría de conxuntos, o axioma da escolla é un axioma que postula que para cada familia de conxuntos non baleiros, existe outro conxunto que contén un elemento de cada un daqueles. De maneira informal, afirma que dada unha colección de «caixas» con obxectos dentro delas, é posible escoller un obxecto de cada caixa. Que este procedemento se pode levar a cabo é trivialmente certo sempre que dita familia sexa finita, ou cando existe unha regra ben determinada que permite «escoller» un único elemento de cada conxunto dela. Con todo, o axioma é indispensable no caso máis xeral dunha familia infinita arbitraria.

Foi formulado en 1904 por Ernst Zermelo, para demostrar que todo conxunto pode ser ben ordenado. Aínda que orixinariamente foi controvertido, hoxe en día é usado sen reservas pola maioría dos matemáticos. Hai aínda, con todo, especialmente na teoría de conxuntos, correntes de opinión que rexeitan o axioma ou que investigan consecuencias doutros axiomas inconsistentes con el.

Enunciado

O enunciado do axioma da escolla afirma que existe unha función de escolla para cada familia de conxuntos non baleiros, é dicir, unha función f tal que para cada conxunto B do seu dominio, f(B) ∈ B. Na teoría de Zermelo-Fraenkel ou similares, o seu enunciado formal é: Modelo:Cita

onde Fun f e Df denotan «f é unha función» e o «dominio de f» en devandita teoría. O axioma da escolla tamén se enuncia de maneiras similares, nas que o siginificado de «función de escolla» varía lixeiramente:

• Toda familia de conxuntos non baleiros F posúe unha función de escolla.
• Para toda familia de conxuntos non baleiros F, o seu produto cartesiano é non baleiro.
• Para todo conxunto A, existe unha función de escolla sobre a colección dos seus subconxuntos non baleiros.
• Para toda familia de conxuntos non baleiros disxuntos dous a dous, F, existe un conxunto D que contén exactamente un elemento de cada conxunto de F: |D ∩ A | = 1, para cada A ∈ F.

Pola contra, a negación do axioma da escolla afirma que existe unha familia de conxuntos —non baleiros— que non posúe ningunha función de escolla.

Uso

Ata finais do século XIX, o axioma da escolla usábase case sempre implicitamente. Por exemplo, despois de demostrar que o conxunto X contiña só conxuntos non baleiros, un matemático diría "sexa F(S) un elemento de S para todo S en X". É en xeral imposible demostrar que F existe sen o axioma da escolla, pero isto non foi notado antes de Zermelo.

Non sempre se require o axioma da escolla. Se X é finito, o axioma necesario dedúcese dos outros axiomas da teoría de conxuntos. En tal caso é equivalente a dicir que se se ten un número finito de caixas, cada unha con polo menos un obxecto, pódese escoller exactamente un obxecto de cada caixa. Isto é evidente: comézase na primeira caixa, escóllese un obxecto; vaise á segunda, escóllese un obxecto; e así sucesivamente. Como só hai finitas caixas, este procedemento de escolla concluirase finalmente. O resultado é unha función de escolla explícita: unha que asigna á primeira caixa o primeiro obxecto escollido, á segunda o segundo etc. Unha proba formal para todo conxunto finito requiriría o principio de indución matemática.

A dificultade aparece cando non hai unha escolla natural de elementos de cada conxunto. Se non se poden facer escollas explícitas, como saber que existe o conxunto desexado? Por exemplo, supóñase que X é o conxunto de todos os subconxuntos non baleiros dos reais. Primeiro poderíase tentar proceder coma se X fose finito; pero se se tenta escoller un elemento de cada conxunto, como X é infinito, o procedemento de escolla non terminará nunca e nunca se poderá producir unha función de escolla para X. Logo pódese tentar o truco de tomar o elemento mínimo de cada conxunto; pero algúns subconxuntos dos reais, como o intervalo aberto (0,1), non teñen mínimo, así que esta táctica non funciona tampouco.

A razón pola que se podían escoller elementos mínimos dos subconxuntos dos naturais é que estes veñen xa ben ordenados: todo subconxunto dos naturais ten un único elemento mínimo respecto á orde natural.

Independencia

Do traballo de Kurt Gödel e Paul Cohen dedúcese que o axioma da escolla é loxicamente independente dos outros axiomas da teoría axiomática de conxuntos. Isto significa que nin o axioma da escolla nin a súa negación se poden demostrar dentro dos axiomas de Zermelo-Fraenkel (ZF), se esa teoría é consistente. En consecuencia, asumir o axioma ou a súa negación nunca levará a unha contradición que non se puidese obter sen ese suposto.

A decisión, entón, de se é ou non apropiado facer uso del nunha demostración non se pode tomar baseándose só noutros axiomas da teoría de conxuntos; hai que buscar outras razóns. Un argumento dado a favor de empregar o axioma da escolla é simplemente que é conveniente: usalo non pode resultar en contradicións e fai posible demostrar algunhas proposicións que doutro xeito non se poderían probar.

O axioma da escolla non é a única afirmación significativa e independente de ZF; a hipótese do continuo xeneralizada (HCX), por exemplo, non só é independente de ZF, senón que o é tamén de ZF co axioma da escolla (ZFE). Con todo, ZF máis HCX necesariamente implica AE, co cal HCX é estritamente máis forte que AE, aínda que ambos sexan independentes de ZF.

Un problema do axioma é que ten como consecuencia a existencia dalgúns obxectos contraintuitivos. Un exemplo diso é o paradoxo de Banach-Tarski, que di basicamente que é posible cortar unha bóla tridimensional en finitas partes, e usando só rotación e translación, reensamblarlas en dúas bólas do mesmo volume que a orixinal. A proba, como todas as probas que involucran o axioma da escolla, é só de existencia: non di como se debe cortar a bóla, só di que se pode facer.

Doutra banda, a negación o axioma é tamén estraña. Por exemplo, a afirmación de que dados dous conxuntos calquera S e T, a cardinalidade de S é menor, igual, ou maior que a de T é equivalente ao axioma da escolla; noutras palabras, se se asume a negación deste, hai dous conxuntos S e T de tamaño incomparable: ningún pode inxectarse no outro.

Unha terceira posibilidade é probar teoremas sen usar nin o axioma nin a súa negación, a táctica preferida nas matemáticas construtivas. Estas afirmacións serán certas en calquera modelo de ZF, independentemente da certeza ou falsidade do axioma da escolla en devandito modelo. Isto fai que calquera proposición que requira AE ou a súa negación sexa indecidible: o paradoxo de Banach-Tarski, por exemplo, non se pode demostrar como certa (pois non se pode descompor a esfera do modo indicado) nin como falsa (pois non se pode demostrar que tal descomposición non exista); esta, con todo, pódese reformular como unha afirmación sobre os modelos de ZF: "en todo modelo de ZF no que valla AE, vale tamén o paradoxo de Banach-Tarski". Así mesmo, todas as afirmacións listadas abaixo que requiren escolla ou algunha versión máis débil son indecidibles en ZF; pero por ser demostrables en ZFE, hai modelos de ZF nos que son certas.

Axiomas máis fortes

O axioma de construtibilidade, igual que a hipótese do continuo xeneralizada, implica o axioma da escolla, pero é estritamente máis forte.

En teorías de clases, tales como a teoría de conxuntos de Von Neumann-Bernays-Gödel ou a de Morse-Kelley, hai un posible axioma chamado axioma da escolla global, que é máis forte que o axioma da escolla para conxuntos pois se aplica tamén a clases propias.

Formas máis febles

Hai varias proposicións máis febles que, aínda que non son equivalentes ao axioma da escolla, están fortemente relacionadas como:

• O axioma da escolla numerable, que di que toda colección numerable de conxuntos non baleiros ten función de escolla. Isto normalmente abonda para probar afirmacións sobre os reais, por exemplo, pois os números racionais, que son numerables, forman un subconxunto denso dos reais.
• O axioma da escolla dependente.

Resultados que requiren AE pero son máis febles

Un dos aspectos máis interesantes do axioma da escolla é o gran número de lugares na matemática nos que aparece. Velaquí algunhas afirmacións que requiren o axioma da escolla no sentido de que non son demostrables en ZF pero si en ZFE. De forma equivalente, estas son certas en todos os modelos de ZFE e falsas nalgúns modelos de ZF.

• Teoría de conxuntos:
  • Toda unión de numerables conxuntos numerables é así mesmo numerable.
  • Se o conxunto A é infinito, existe unha función inxectiva do conxunto dos naturais ℕ en A.
• Teoría da medida:
  • Existen subconxuntos dos reais que non teñen medida de Lebesgue, como o conxunto de Vitali.
  • O paradoxo de Hausdorff.
  • O paradoxo de Banach-Tarski.
• Álxebra:
  • Todo corpo ten clausura alxébrica.
  • Todo subgrupo dun grupo libre é tamén libre (teorema de Nielsen-Schreier).
  • Os grupos aditivos ℝ e ℂ son isomorfos.
• Teoría da orde:
  • Todo conxunto pode ser linearmente ordenado.
• Álxebra de Boole:
  • Todo filtro nunha álxebra de Boole pode ser estendido a un ultrafiltro.
• Análise funcional:
  • O teorema de Hahn-Banach en análise funcional, que permite a extensión de funcionais lineares.
  • Todo espazo de Hilbert ten unha base ortonormal.
  • O teorema da categoría de Baire sobre espazos métricos completos, e as súas consecuencias.
  • En todo espazo vectorial topolóxico de dimensión infinita hai unha función linear descontinua.
• Topoloxía:
  • Un espazo uniforme é compacto se e só se é completo e totalmente limitado.
  • Todo espazo de Tychonoff ten unha compactificación de Stone-Čech.

Resultados que requiren AE

Hai modelos da teoría de Zermelo-Fraenkel nos que o axioma da escolla; abréviase "teoría de conxuntos de Zermelo-Fraenkel máis a negación do axioma da escolla" por ZF¬E. Nalgúns modelos de ZF¬E é posible probar a negación dalgunhas propiedades comúns, e posto que un modelo de ZF¬E é tamén modelo de ZF, cada unha das seguintes afirmacións é válida nalgún modelo de ZF (supondo, como sempre, que ZF é consistente):

• Existe un modelo de ZF¬E no que hai unha función f dos reais nos reais que non é continua en a, pero para toda sucesión {x_n} que converxa a a, f(x_n) converxe a f(a).
• Existe un modelo de ZF¬E no que o conxunto dos reais é unha unión numerable de conxuntos numerables.
• Existe un modelo de ZF¬E no que hai un corpo sen clausura alxébrica.
• En todos os modelos de ZF¬E hai un espazo vectorial sen base.
• Existe un modelo de ZF¬E no que hai un espazo vectorial con dúas bases de cardinalidade diferente.
• Existe un modelo de ZF¬E no que todo subconxunto de Rⁿ é medible. Con isto é posible eliminar resultados contraintuitivos como o paradoxo de Banach-Tarski, que son demostrables en ZFE.
• En ningún modelo de ZF¬E vale a hipótese do continuo xeneralizada.

Véxase tamén

Bibliografía

• Modelo:Cita libro
• Modelo:Cita publicación periódica
• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita libro
• Modelo:Cita publicación periódica Reimpreso con tradución ao inglés en Modelo:Harvsp, e tradución ao inglés en Modelo:Harvsp.
• Modelo:Cita publicación periódica Reimpreso con tradución ao inglés en Modelo:Harvsp, e tradución ao inglés en Modelo:Harvsp.
• Modelo:Cita libro